Complex Networks
Complex Networks
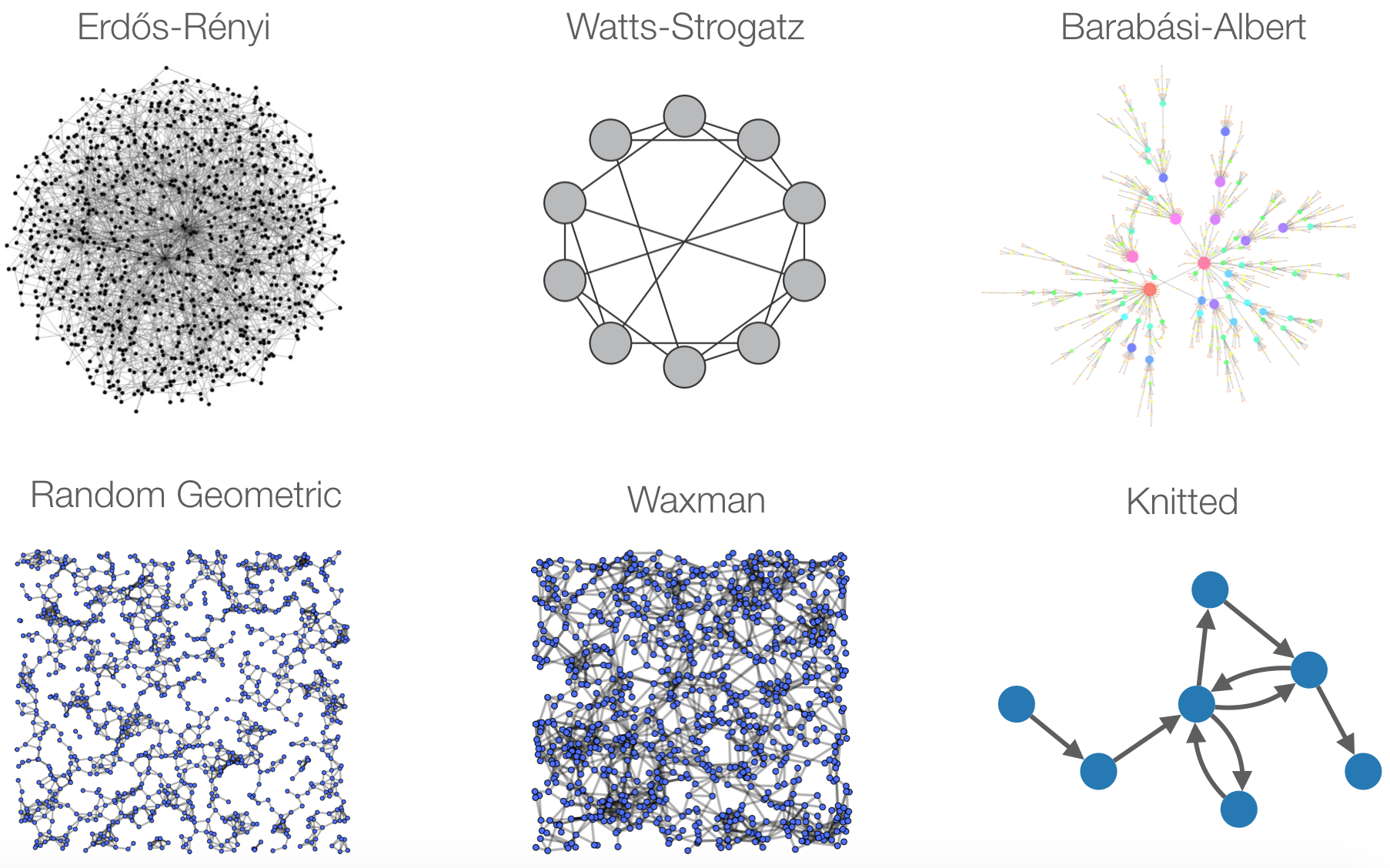
Although the concept of a graph is very old, recent advances on the use of such structures to model real-world systems gave rise to a new research area known as Network Science, in which a graph is commonly called a complex network. Almost any discrete system can be represented as a complex network. Therefore, the tools from Network Science can be used on a diverse range of research areas such as genetics, social sciences, linguistics and particle physics. Although we are open to work with any application of complex networks, our current research is focused on two main topics:
Urban networks
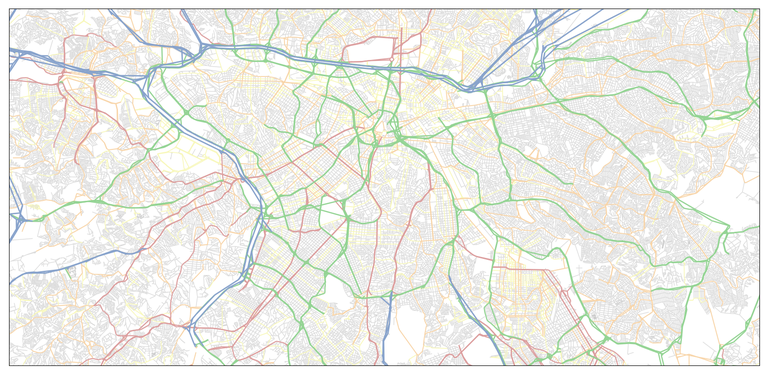
The ever-increasing availability of data about many aspects of urban life has given rise to an equally booming research field regarding city characterization and modeling. Traffic dynamics, pedestrian movement, social interactions, criminality analysis and physical growth are only a few of the many topics that can investigated. A powerful tool that can be used for such a task is network theory. We are particularly interested in modeling the street network of cities, which can be regarded as a fundamental correlate of city organization, growth and development. Such a system has a natural representation as a graph, which allows the immediate application of many concepts from network theory. Our long-term goal is to define a measure for city complexity based on the respective graph representation.
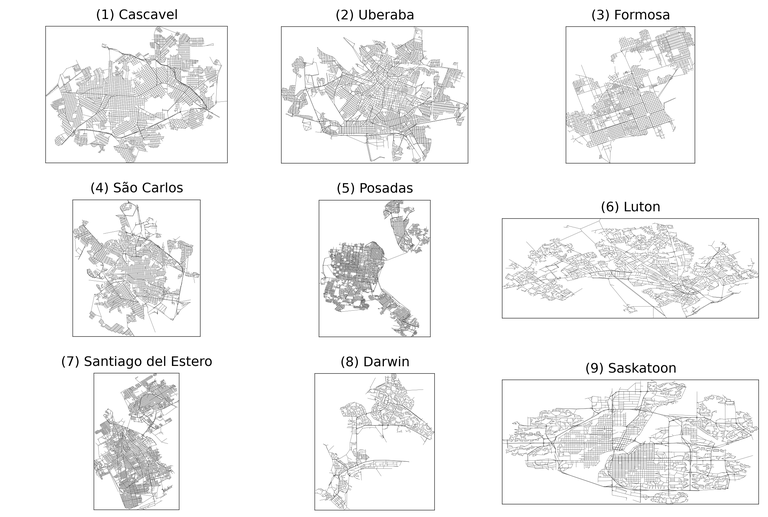
Selected publication
- Cesar H. Comin, Filipi N. Silva, and Luciano da F. Costa. “A diffusion-based approach to obtaining the borders of urban areas.” Journal of Statistical Mechanics: Theory and Experiment 2016, no. 5 (2016): 053205.
- Domingues, Guilherme S., Filipi N. Silva, Cesar H. Comin, and L. da F Costa. "Topological characterization of world cities." Journal of Statistical Mechanics: Theory and Experiment 2018, no. 8 (2018): 083212.
Dynamics on networks
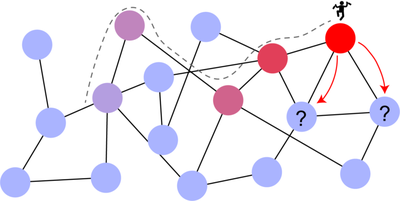
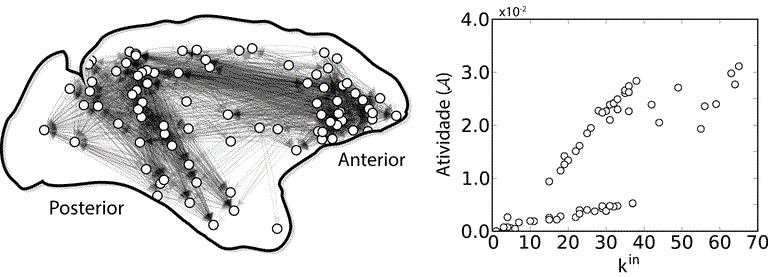
Processes taking place on networks, such as epidemic spreading, traffic flow and packet routing, can be characterized and modeled using tools from network science. Among the many dynamics that have been studied in the literature, random walks are probably one of the most fundamental. The random walk dynamics underlies a large number of models in physics, biology, sociology and many other areas. For instance, in network theory this dynamics is the base of the so-called Google’s page rank algorithm. Therefore, the study of random walks on heterogeneous media, such as graphs, can lead to exciting new models and applications. One of the most important properties of a random walk is the number of times that the walker passes through a node, which can be called the activity of that node. For directed graphs, random walks possess many non-trivial behaviors such as the possibility of getting “trapped” into a set of nodes, which can lead to large fluctuations on the activity of the nodes. A current investigation from our group is the identification of topological properties that can lead to the correct prediction of a node’s activity on directed graphs. If successful, such a prediction can lead to improvements of many real-world systems such as city traffic, packet routing in the internet and even provide a better understanding of brain dynamics.
Selected publications
- Cesar H. Comin, Mateus P. Viana, Lucas Antiqueira, and Luciano da F Costa. “Random walks in directed modular networks.” Journal of Statistical Mechanics: Theory and Experiment 2014, no. 12 (2014): P12003.
- Filipi N. Silva, Cesar H. Comin, Thomas K. DM Peron, Francisco A. Rodrigues, Cheng Ye, Richard C. Wilson, Edwin R. Hancock, and Luciano da F. Costa. “Concentric network symmetry.” Information Sciences 333 (2016): 61-80.