Neuromorphology and physiology
Morphology and dynamics of neurons

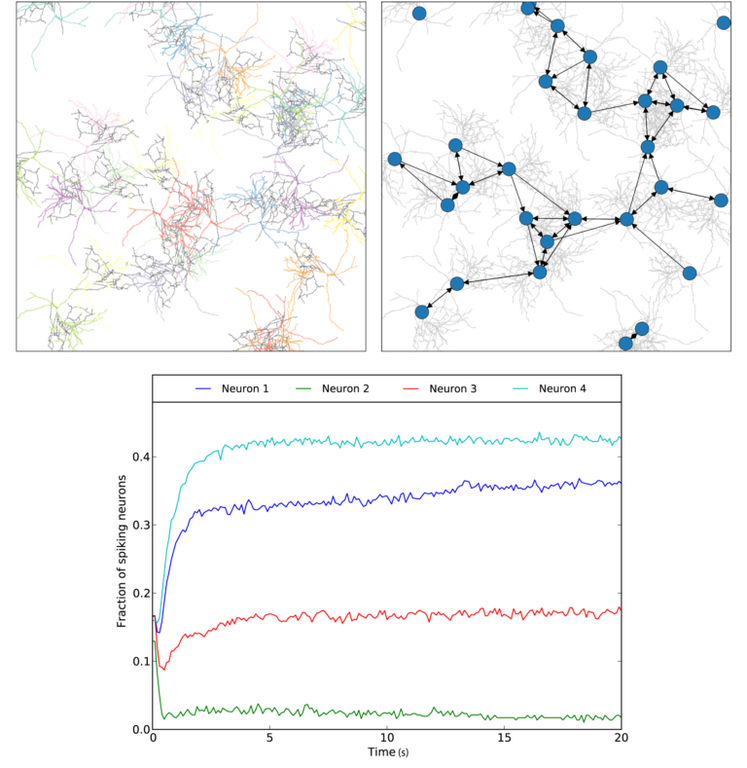
There are approximately 85 billion neurons in the human brain. A neuron may be connected to as many as 10000 other neurons, originating an intricate web of connections that can propagate trillions of spiking signals. To some degree, such a connectivity is a result of the morphology, or shape, of the neurons. For instance, neurons having longer dendrites can connect to far away neurons better than neurons possessing shorter dendrites, although this capability tends to imply in a higher metabolic cost.
Our interest lies on distinct, but interrelated, aspects of neuronal systems. The first aspect is the categorization of neurons according with their respective morphology, a pattern recognition task. The aim is to identify typical morphological properties of known neuronal classes such as pyramidal and GABAergic neurons, as well as to identify new morphological categories of neurons. The second aspect involves the prediction of the connectivity given the morphological properties of a neuron. The basic approach is to construct a network of connections from an ensemble of selected neuronal shapes and analyze properties of the resulting network. The third aspect deals with studying the propagation of signals in the neural network. The main objective lies on identifying the relationship between the morphology, connectivity and dynamics of neuronal systems.
Selected articles
- Cesar H. Comin, and Luciano da F. Costa. “Shape, connectedness and dynamics in neuronal networks.” Journal of neuroscience methods 220, no. 2 (2013): 100-115.
- Cesar H. Comin, Julian Tejada, Matheus P. Viana, Antonio C. Roque, and Luciano da F. Costa. “Archetypes and Outliers in the Neuromorphological Space.” In The Computing Dendrite, pp. 41-59. Springer New York, 2014.
- Cesar H. Comin, Joao LB Batista, Matheus P. Viana, Luciano Da F. Costa, Bruno AN Travencolo, and Marcus Kaiser. “Structure and dynamics: the transition from nonequilibrium to equilibrium in integrate-and-fire dynamics.” International Journal of Bifurcation and Chaos 22, no. 07 (2012): 1250174.